25th November 2020

Deep inside the LEO 1 computer (and the one you are using to read this), there are electronic units called a 'half-adder'.  But what is the half adder and why would it feature in the VR version of the LEO 1 computer?

In the first of two blogs, I will attempt to explain a little more about what this fundamental device is and how it was constructed as part of LEO 1.

Take a deep breath because we have to do some arithmetic first if we are to understand the function of a half adder.  Imagine you are adding up two ordinary numbers;  for example, 1253 + 2589.  Now look carefully at the column second from the right as an example,  I have circled it in red.   

You have to add 5 and 8 to get 13 and then add anything that was carried over from the first column on the right.  The carry was a 1,  from 3 + 9 = 12.  So 13 + 1 = 14.  We leave the 4 in that column as an answer and carry the one onto the next column to the left. 

In each column we have to do two additions;   addition 1 - add the two numbers in the column,  addition 2 - add any carry from the previous column.  If we only add up the two numbers in the column (addition 1) then we are only doing half the job,  we have performed a half addition,  we have been a 'half-adder'.

If we do both additions in that column, that is add the two numbers and then add any carry,  then we have done the whole job, so we can call ourselves a 'full adder'.

Some people of course are good at adding up columns of numbers,  sometimes a lot more than the two in my example.  But if you analyse what they do,  you will find them adding in 'pairs'. We learn that, for example, 6 + 7 = 13,  because we know our number bonds.  But these tend to be restricted to two numbers.  If I asked you what is 2 + 9 + 4,  you would break that into pairs;  ie  2 + 9 = 11 and then 11 + 4 = 15.  Computers also work in pairs but don't have to 'know' very many number bonds.  The computer works in binary (base 2) and has only to worry about ones and zeros.  So in any column of 'bits', the computer can only be faced with 4 combinations,  presented below.

Our 'half-adder'  inside the computer needs to be able to take the two inputs (the two binary digits) and through some clever electronics,  generate the answer plus any carry.  The device that can do this is called the half adder and is fundamental to the way a computer works,  in the past and still today.

Of course, to fully add any column,  we have to take into account the carry from the previous column.  In this case, we have to do 'addition 2' and so we have a choice.   We can use a second half-adder and the pair of two half adders make a full adder.  In the past we might have also used the same half adder twice with a delay, between each addition,  to finally get the answer and carry we desire.

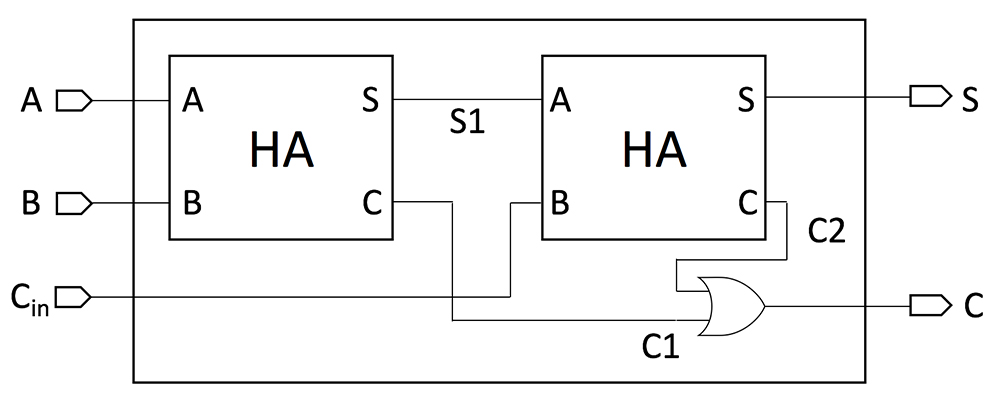The diagram above shows two half adders (HA) being used together to make a full adder.  A and B are the two bits being added in any one column,  with Cin as the carry from the previous column. On the output side,  S is the sum for that column, and C the carry to take to the next column.

The ability to add two binary 'bits' and find the sum plus the carry is absolutely critical to the way a computer works.  For almost all of what your computer does today,  somewhere deep inside a half adder is very busy at work, adding those two simple bits. 

Mathematicians can describe the way a half adder works through the use of 'logic gates' and the diagram below shows a half adder expressed as the connections between logic gates.  

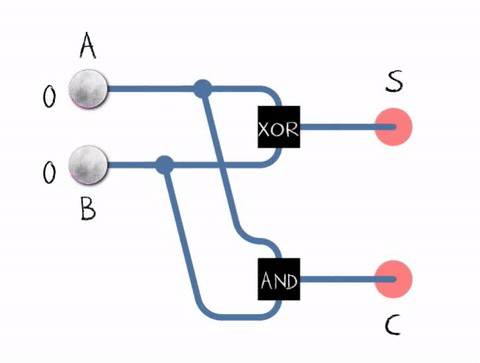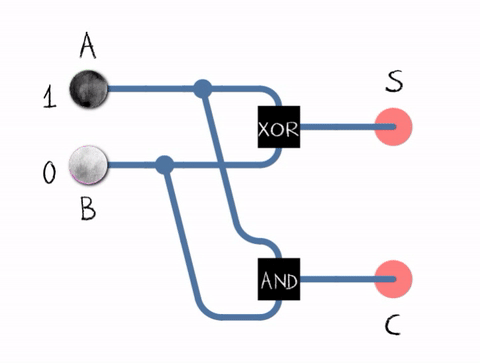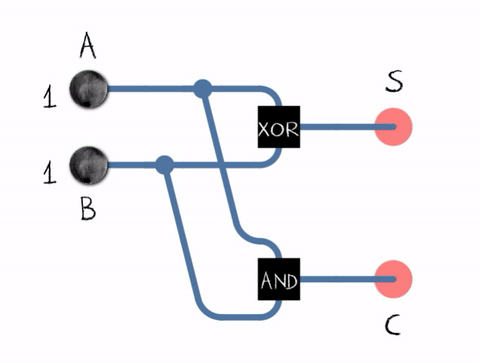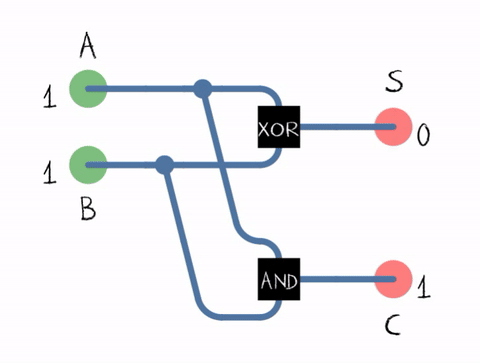
Wikipedia has lots more about different types of adders here: 

So,  if I opened up a half adder,  would I expect to find tiny logic gates?   No! logic gates are just concepts defined by us to express what happens when two or more inputs combine and produce an output.  In reality, the science of electronics has to enable us to build devices that can simulate the function of a logic gate.  Today's electronics offers us very tiny devices called transistors that suitably combined with some other devices,  can be made to perform the function of a logic gate and hence a half adder.  For LEO 1 in the late 1940s,  the key component was the 'thermionic valve' and with supporting components,  could be assembled into units that performed the function of logic gates and ultimately the half adder.  

The photograph below is of a LEO 1 half-adder,  currently in store at Birmingham Museum.   By today's standards, it is huge,  but it would enable the LEO 1 computer to add two bits together and from there perform many and varied calculations to assist Lyons and other organisations in their day to day work.

The half adder really is the 'lego brick' of the computer and we are lucky that an example of one that worked in LEO 1 is still available for study.  It is one of the most important units to be found in the LEO 1 racks and we hope to visualise it for the virtual version of the LEO 1 computer at Cadby Hall.

Next time we will look more closely at the LEO 1 half adder and how the analogue electronics of that time were used to perform the digital function of logic gates.